Kakuro – Einfach
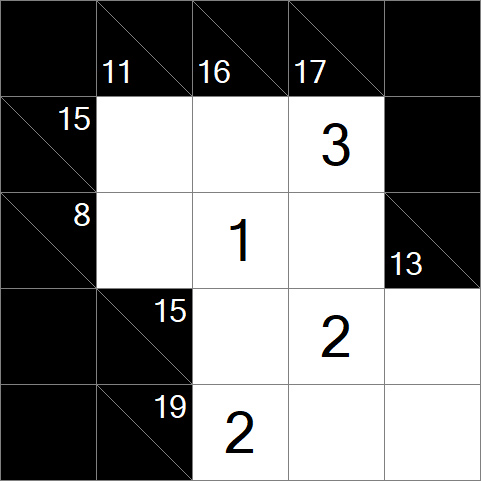
Puzzle & Lösung herunterladen
Puzzle teilen
Unsere Puzzles sind völlig kostenlos. Bitte unterstütze diese Website, indem du sie deinen Freunden und Bekannten weiterempfiehlst. Danke!
Neues Puzzle
Über Kakuro
Kakuro, auch bekannt als "Kreuzsummen" oder "Additionskreuzworträtsel", ist ein mathematisches Rätsel, das Ihre Additionsfähigkeiten und logisches Denken herausfordert. Das Spiel wird typischerweise auf einem Gitter gespielt, ähnlich einem Kreuzworträtsel, mit leeren Feldern, die mit Zahlen gefüllt werden müssen. Das Ziel ist es, alle leeren Felder mit den Zahlen 1-9 zu füllen, sodass die Summe der Zahlen in jeder horizontalen und vertikalen Reihe den gegebenen Hinweisen entspricht, und dabei sicherzustellen, dass keine Zahl innerhalb einer einzelnen Reihe wiederholt wird. Die Hinweise sind in schwarzen Feldern gegeben und geben die Summe für die angrenzenden weißen Felder an. Kakuro-Rätsel können von relativ einfach bis hochkomplex reichen und bieten eine unterhaltsame und ansprechende Möglichkeit, sich mit Mathematik und Logik zu beschäftigen.
Verständnis des Rätsels:
- Gitterstruktur:
- Kakuro-Rätsel werden auf einem Gitter aus Zellen gespielt, von denen einige schwarze Felder enthalten.
- Die schwarzen Felder enthalten "Hinweise" in Form von kleinen Zahlen, entweder oben, unten oder in der Ecke des Feldes.
- Hinweise:
- Die Zahlen in den schwarzen Feldern sind die "Hinweise", die Ihnen die Summe der Zahlen mitteilen, die Sie in die angrenzenden weißen Felder eingeben müssen.
- Ein Hinweis könnte sich horizontal (auf die Reihe weißer Felder zu seiner Rechten) oder vertikal (auf die Spalte weißer Felder unter ihm) beziehen.
Grundregeln:
- Zahlenplatzierung:
- Füllen Sie die weißen Felder mit Zahlen zwischen 1 und 9.
- Summe muss übereinstimmen:
- Die Summe der Zahlen in jeder horizontalen oder vertikalen Reihe weißer Felder muss dem Hinweis entsprechen, ohne Wiederholung von Zahlen.
- Keine Wiederholung:
- Zahlen dürfen innerhalb einer einzelnen Reihe (horizontal oder vertikal) nicht wiederholt werden.
Lösungsstrategien:
- Beginnen Sie mit einzelnen Hinweisen:
- Identifizieren Sie Reihen oder Spalten, bei denen nur eine mögliche Kombination von Zahlen zur Verfügung steht, die dem Hinweis entspricht und den Regeln entspricht.
- Verwenden Sie Querverweise:
- Suchen Sie nach Stellen, an denen sich Reihen und Spalten kreuzen, und verwenden Sie die Hinweise von beiden, um die Möglichkeiten einzugrenzen.
- Verwenden Sie Eliminierung:
- Identifizieren Sie Zahlen, die unmöglich in einen bestimmten Raum passen können, und eliminieren Sie sie als Optionen.
- Suchen Sie nach eindeutigen Lösungen:
- Manchmal hat eine bestimmte Reihe von Feldern nur eine mögliche Kombination von Zahlen, die funktioniert. Identifizieren Sie diese frühzeitig, um das Lösen zu erleichtern.
- Verwenden Sie Subtraktion:
- Manchmal kann das Subtrahieren der Gesamtzahl bekannter Zahlen vom Hinweis Ihnen helfen, die fehlenden Zahlen zu finden.
- Arbeiten Sie mit definitiven Feldern:
- Versuchen Sie immer, Felder auszufüllen, bei denen Sie sich der Zahl sicher sind, und verwenden Sie diese, um angrenzende Reihen zu lösen.
- Verwenden Sie Bleistiftmarkierungen:
- Wie beim Sudoku können Sie kleine Bleistiftmarkierungen möglicher Zahlen in einem Feld machen und diese aktualisieren, wenn Sie mehr Informationen erhalten.
- Überprüfen Sie während des Vorgangs:
- Überprüfen Sie regelmäßig, ob die Zahlen, die Sie bisher platziert haben, allen Regeln und Hinweisen entsprechen.
- Suchen Sie nach Mustern:
- Wenn Sie erfahrener werden, werden Sie anfangen, Muster und Kombinationen zu erkennen, die häufig auftreten, was Ihr Lösen beschleunigen kann.
- Verwenden Sie Logik, nicht Raten:
- Stellen Sie sicher, dass jede von Ihnen platzierte Zahl durch Logik und Eliminierung und nicht durch Raten gestützt ist.
Beispiel:
- Wenn Sie eine Reihe von zwei Feldern mit einem Hinweis von 3 haben, ist die einzige mögliche Kombination 1 und 2.
- Wenn Sie eine Reihe von drei Feldern mit einem Hinweis von 6 haben und Sie wissen, dass eines der Felder eine 1 ist, müssen die anderen beiden 2 und 3 sein.
Fortgeschrittene Techniken:
- Überlappungsmethode:
- Manchmal kann das Betrachten des überlappenden Abschnitts zweier Reihen Einblicke in die möglichen Zahlen geben.
- Kombinationsanalyse:
- Das Analysieren möglicher Kombinationen in größeren Reihen kann manchmal dazu beitragen, die einzige mögliche Platzierung bestimmter Zahlen zu identifizieren.