Sohei Sudoku – Einfach

Um mehrere Puzzles gleichzeitig auszudrucken, klicke hier.

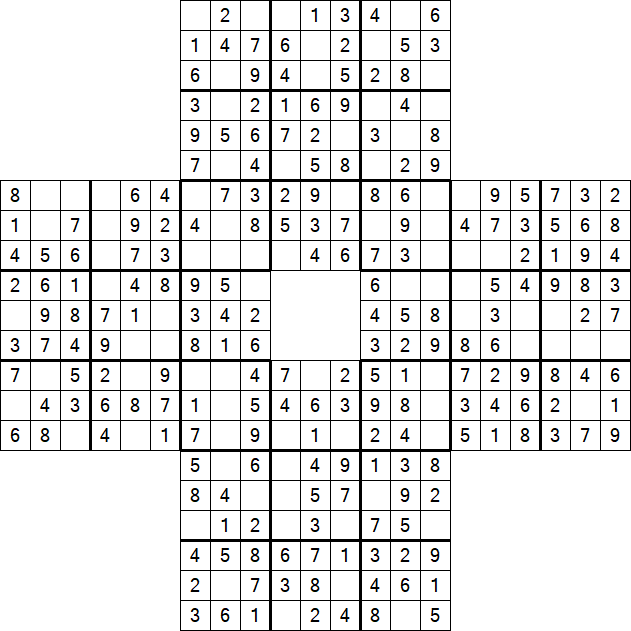
Sohei Sudoku ist eine Variante des klassischen Sudoku und ist nach den Kriegermönchen (Sohei) des mittelalterlichen Japans benannt. Dieses Rätsel besteht aus vier einzelnen Sudoku-Gittern, die so miteinander verschmolzen sind, dass sie einige Regionen miteinander teilen und so ein größeres, miteinander verbundenes Rätsel schaffen. Jedes Gitter hat zwei überlappende Bereiche mit benachbarten Gittern, was den Lösungsprozess verknüpft und von den Lösungen der benachbarten Gitter abhängig macht.

Grundregeln

1. Gitterstruktur: Das Rätsel besteht aus vier 9x9 Gittern, jedes mit seinen eigenen Reihen, Spalten und Boxen.
2. Zahlen 1-9: Jede Reihe, jede Spalte und jede 3x3 Box innerhalb jedes 9x9 Gitters muss die Zahlen 1 bis 9 enthalten, ohne Wiederholung.
3. Überlappende Bereiche: Die Gitter sind durch überlappende Bereiche verbunden, die die Regeln in allen miteinander verbundenen Gittern befolgen müssen.

Zusätzliche Regeln

• Verknüpfte Lösungen: Die überlappenden Bereiche bedeuten, dass das Lösen eines bestimmten Bereichs in einem Gitter die Lösungen im benachbarten Gitter beeinflusst. Die Zahlen in den überlappenden Bereichen müssen die Sudoku-Regeln für beide Gitter, zu denen sie gehören, befolgen.

Grundlegende Lösungstipps

• Beginne mit gegebenen Zahlen: Konzentriere dich zunächst auf die Gitter oder Einheiten mit den meisten vorgegebenen Zahlen, da sie den einfachsten Ausgangspunkt für die Bestimmung des Platzes anderer Zahlen bieten.
• Achte auf Überlappungen: Achte besonders auf die überlappenden Bereiche zwischen den Gittern, da diese entscheidende Verbindungen zwischen den Lösungen verschiedener Gitter bieten.
• Verwende klassische Strategien: Nutze klassische Sudoku-Strategien, wie die Suche nach Einzelzahlen, zeigenden Paaren und Box-Line-Reduktion, innerhalb jedes einzelnen Gitters.
• Verknüpfte Lösung: Denke daran, dass das Lösen eines Bereichs in einem Gitter die möglichen Lösungen im benachbarten Gitter beeinflusst. Überprüfe immer die Auswirkungen des Platzierens einer Zahl in den überlappenden Bereichen auf beide Gitter.
• Bewahre Konsistenz: Stelle sicher, dass die Lösungen in allen miteinander verbundenen Gittern, insbesondere in den überlappenden Bereichen, konsistent sind.