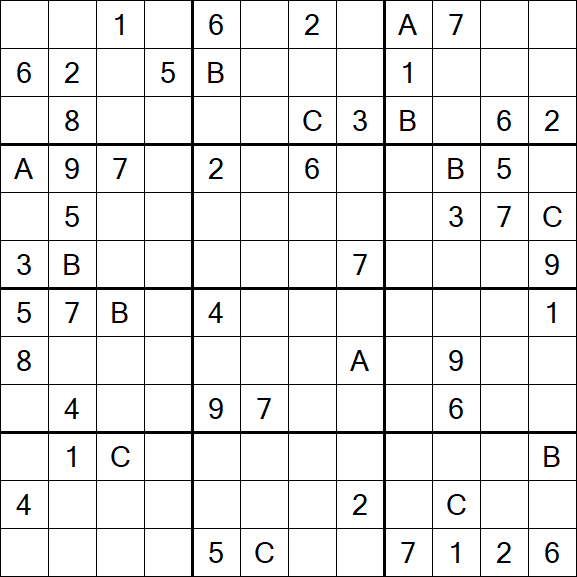
Sudoku 12×12 – Schwierig

Um mehrere Puzzles gleichzeitig auszudrucken, klicke hier.

Sudoku 12x12 ist eine Variante des klassischen Sudoku-Rätsels, jedoch mit einem größeren Gitter und zusätzlichen Zahlen. Das Gitter besteht aus einer 12x12-Matrix, die weiter in 4x3-Untergitter oder Regionen unterteilt ist. Einige Zellen im Gitter sind bereits mit Zahlen gefüllt, die als Hinweise dienen, um das Rätsel zu lösen.

Grundregeln

1. Gitterstruktur: Das Rätsel besteht aus einem 12x12 Gitter, unterteilt in 4x3 Regionen.
2. Verwendete Zahlen: Die Zahlen 1 bis 12 werden verwendet, um das Gitter zu füllen.
3. Vorausgefüllte Zahlen: Einige Zellen sind vorausgefüllt, um als Hinweise zu dienen.
4. Ziel: Fülle die leeren Zellen mit Zahlen, sodass keine Wiederholung in einer Reihe, Spalte oder Region erfolgt.

Zusätzliche Regeln

• Einzigartige Zahlen: Jede Zahl von 1 bis 12 muss genau einmal in jeder Reihe, Spalte und definierten Region erscheinen.
• Keine Wiederholung: Keine Zahl darf in einer einzelnen Reihe, Spalte oder Region wiederholt werden.

Grundlegende Lösungstipps

1. Einzige Möglichkeit: Wenn eine Zelle die einzige in ihrer Reihe, Spalte oder Region ist, die eine bestimmte Zahl enthalten kann, muss sie diese Zahl enthalten.
2. Eliminierung: Schließe Zahlen für eine bestimmte Zelle aus, basierend auf den Zahlen, die bereits in der Reihe, Spalte und Region dieser Zelle vorhanden sind.
3. Doppelte Paare: Wenn zwei Zellen in einer Reihe, Spalte oder Region nur zwei Zahlen (ein Paar) sein können, können diese beiden Zahlen für andere Zellen in dieser Reihe, Spalte oder Region ausgeschlossen werden.
4. Suche nach Gittersymmetrie: Manchmal kann die Anordnung der gegebenen Zahlen ein symmetrisches Muster haben, das bei der Vorhersage der Platzierung anderer Zahlen hilft.
5. Mit Sicherheit arbeiten: Beginne mit dem Ausfüllen von Zahlen, bei denen du dir sicher bist, und bewege dich dann zu den wahrscheinlichen.