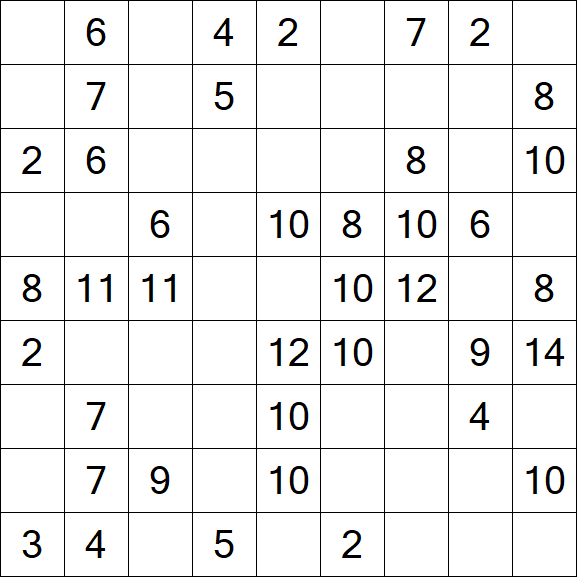
Kuromasu – Einfach

Um mehrere Puzzles gleichzeitig auszudrucken, klicke hier.

Kuromasu, auch bekannt als "Kurodoko," ist ein Logikrätsel aus Japan. Es wird auf einem rechteckigen Gitter gespielt, in dem einige Zellen Zahlen enthalten. Die Hauptaufgabe besteht darin, zu entscheiden, ob jede Zelle schwarz gefärbt oder weiß gelassen werden sollte.

Grundregeln

1. Das Gitter besteht aus Zellen, die entweder schwarz gefärbt oder weiß gelassen werden können.
2. Einige Zellen enthalten bereits Zahlen, die Hinweise für die Lösung geben.
3. Die Zahlen in den Zellen geben an, wie viele weiße Zellen, einschließlich der nummerierten Zelle selbst, horizontal oder vertikal von dieser Zelle aus gesehen werden können.
4. Eine Zelle gilt als "sichtbar", wenn sie sich in der gleichen Zeile oder Spalte befindet und keine schwarzen Zellen den Blick versperren.

Zusätzliche Regeln

1. Zellen mit Zahlen dürfen nicht schwarz sein.
2. Schwarze Zellen dürfen nicht horizontal oder vertikal nebeneinander liegen.
3. Alle weißen Zellen müssen eine einzige zusammenhängende Gruppe bilden, d.h. jede weiße Zelle muss horizontal oder vertikal an eine andere weiße Zelle angrenzen.

Grundlegende Lösungstipps

1. Startpunkt: Beginnen Sie mit den Zellen mit hohen Zahlen. Diese geben Hinweise auf lange Reihen von verbundenen weißen Zellen.
2. Schwarze Zellenblocker: Wenn das Färben einer Zelle in Schwarz den Blick auf eine nummerierte Zelle blockiert, die ihre erforderliche Anzahl nicht erreichen kann, dann muss sie weiß bleiben.
3. Weiße Zellenverbinder: Achten Sie darauf, dass alle weißen Zellen verbunden bleiben. Suchen Sie nach Zellen, die, wenn sie schwarz wären, eine Gruppe von weißen Zellen isolieren würden. Solche Zellen müssen weiß bleiben.
4. Angrenzungsregel: Wenn festgestellt wird, dass eine Zelle aufgrund der obigen Hinweise weiß ist, werden alle angrenzenden Zellen schwarz sein, da zwei schwarze Zellen nicht nebeneinander liegen dürfen.