Sudoku 12×12 – Moyen

Pour imprimer plusieurs puzzles en même temps, clique ici.

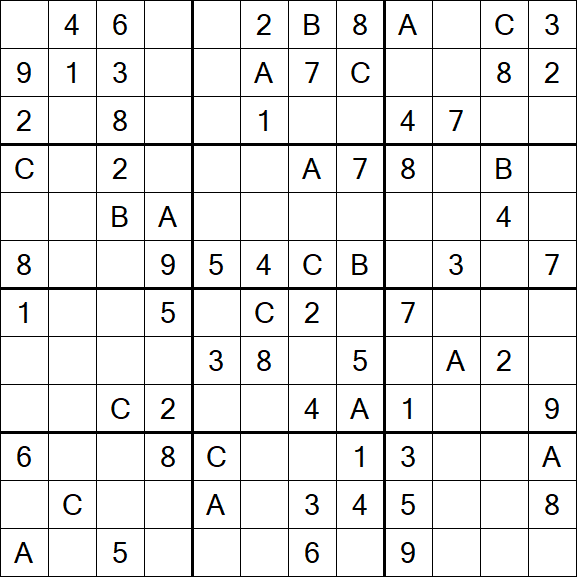
Le Sudoku 12x12 est une variante du classique Sudoku, mais avec une grille plus grande et des nombres supplémentaires à placer. La grille est composée d'une matrice 12x12, qui est ensuite divisée en sous-grilles 4x3, également connues sous le nom de régions. Certaines cellules de la grille sont pré-remplies avec des nombres, servant d'indices pour aider à résoudre le puzzle.

Règles de Base

1. Structure de la Grille: Le puzzle est composé d'une grille de 12x12, subdivisée en régions de 4x3.
2. Nombres Utilisés: Les nombres de 1 à 12 sont utilisés pour remplir la grille.
3. Nombres Pré-remplis: Certaines cellules sont pré-remplies pour servir d'indices.
4. Objectif: Remplir les cellules vides avec des nombres en veillant à ne pas répéter de nombre dans chaque ligne, colonne ou région.

Règles Supplémentaires

• Nombres Uniques: Chaque nombre de 1 à 12 doit apparaître exactement une fois dans chaque ligne, colonne et région définie.
• Pas de Répétition: Aucun nombre ne peut être répété dans une seule ligne, colonne ou région.

Astuces de Base pour Résoudre

1. Possibilité Unique: Si une cellule est la seule dans sa ligne, colonne ou région qui peut contenir un nombre particulier, alors elle doit contenir ce nombre.
2. Élimination: Excluez les nombres pour une cellule particulière en fonction des nombres déjà présents dans la ligne, la colonne et la région de cette cellule.
3. Paires Doubles: Si deux cellules dans une ligne, colonne ou région ne peuvent être que deux nombres (une paire), alors ces deux nombres peuvent être exclus pour les autres cellules dans cette ligne, colonne ou région.
4. Recherche de Symétrie de Grille: Parfois, l'arrangement des nombres donnés peut avoir un motif symétrique qui peut aider à prédire la placement des autres nombres.
5. Travailler avec Certitude: Commencez par remplir les nombres dont vous êtes sûr, puis passez aux nombres probables.