Sudoku DG – Fácil

Para imprimir vários quebra-cabeças ao mesmo tempo, clique aqui.

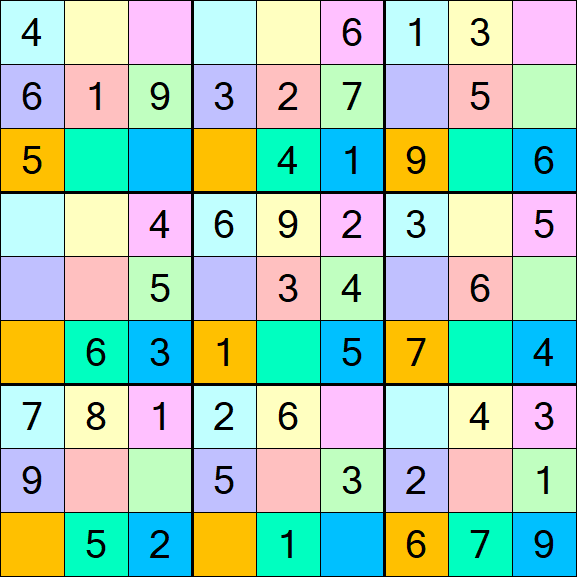
O Sudoku-DG, também conhecido como "Sudoku Deslocado", é uma variante do clássico Sudoku, um quebra-cabeça de colocação de números. A grade tradicional do Sudoku consiste em uma matriz 9x9, subdividida em subgrades 3x3, referidas como "regiões". Algumas células são pré-preenchidas com números, chamados de "dados". O objetivo é preencher as células vazias de tal forma que cada linha, coluna e região contenha os números de 1 a 9, com cada número aparecendo exatamente uma vez. O nome "Sudoku" implica "números únicos", pois cada número deve aparecer apenas uma vez em cada uma das três "direções" (linha, coluna e região).

Regras Básicas

1. Estrutura da Grade: O quebra-cabeça apresenta uma grade 9x9, dividida em regiões 3x3.
2. Dados: Algumas células são pré-preenchidas com números, conhecidos como "dados".
3. Colocação de Números: Cada linha, coluna e região deve conter os números de 1 a 9 sem repetição.

Regras Adicionais para o Sudoku-DG

1. Grupos Disjuntos: Além das regras básicas do Sudoku, o Sudoku-DG introduz 9 grupos disjuntos, cada um correspondendo a uma posição relativa de caixa dentro das regiões e destacado com uma cor distinta.
2. Numeração dos Grupos: Cada grupo colorido de 9 células também deve conter os dígitos de 1 a 9 sem repetição.

Dicas Básicas de Resolução

• Possibilidade Única: Se uma célula é a única em sua linha, coluna ou região que pode conter um número particular, então ela deve conter esse número.
• Candidato Único: Se um número é candidato em apenas uma célula de uma linha, coluna ou região, então essa célula deve conter esse número.
• Eliminação: Exclua números das células com base nos números já presentes em uma linha, coluna ou região particular.
• Consideração de Grupos Disjuntos: Preste atenção aos grupos coloridos e certifique-se de que os números de 1 a 9 apareçam em cada grupo disjunto sem repetição.