Sudoku DG – Difficile
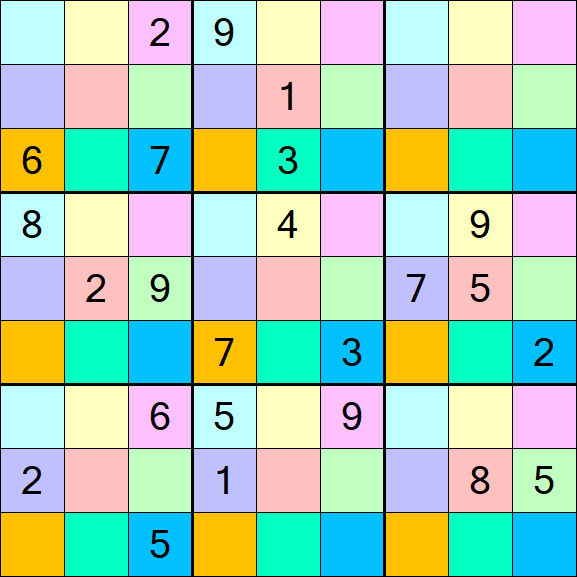
Télécharger puzzle & solution
Partager le puzzle
Nos puzzles sont entièrement gratuits. Merci de soutenir ce site en le recommandant à tes amis et connaissances. Merci !
Nouveau puzzle
À propos du Sudoku DG
Le Sudoku-DG, également connu sous le nom de "Sudoku Décalé", est une variante du Sudoku classique, un puzzle de placement de nombres. La grille de Sudoku traditionnelle est composée d'une matrice 9x9, subdivisée en sous-grilles 3x3, appelées "régions". Certaines cellules sont pré-remplies avec des nombres, appelés "données". L'objectif est de remplir les cellules vides de manière à ce que chaque ligne, colonne et région contienne les nombres de 1 à 9, chaque nombre apparaissant exactement une fois. Le nom "Sudoku" implique "nombres uniques" car chaque nombre ne doit apparaître qu'une seule fois dans chacune des trois "directions" (ligne, colonne et région).
Règles de Base
- Structure de la Grille: Le puzzle comporte une grille de 9x9, divisée en régions de 3x3.
- Données: Certaines cellules sont pré-remplies avec des nombres, appelés "données".
- Placement des Nombres: Chaque ligne, colonne et région doit contenir les nombres de 1 à 9 sans répétition.
Règles Supplémentaires pour le Sudoku-DG
- Groupes Disjoints: En plus des règles de base du Sudoku, le Sudoku-DG introduit 9 groupes disjoints, chacun correspondant à une position de boîte relative dans les régions et mis en évidence par une couleur distincte.
- Numérotation des Groupes: Chaque groupe de 9 cellules de même couleur doit également contenir les chiffres de 1 à 9 sans répétition.
Astuces de Base pour Résoudre
- Possibilité Unique: Si une cellule est la seule dans sa ligne, colonne ou région à pouvoir contenir un nombre particulier, alors elle doit contenir ce nombre.
- Candidat Unique: Si un nombre est candidat dans une seule cellule d'une ligne, colonne ou région, alors cette cellule doit contenir ce nombre.
- Élimination: Excluez les nombres des cellules en fonction des nombres déjà présents dans une ligne, colonne ou région particulière.
- Considération des Groupes Disjoints: Portez attention aux groupes colorés et assurez-vous que les nombres de 1 à 9 apparaissent dans chaque groupe disjoint sans répétition.