Sohei Sudoku – Difícil
Baixar Puzzle & Solução
Compartilhar quebra-cabeça
Nossos quebra-cabeças são completamente livres. Por favor, apoie este site recomendando-o a seus amigos e familiares. Obrigado!
Novo quebra-cabeça
Sobre Sohei Sudoku
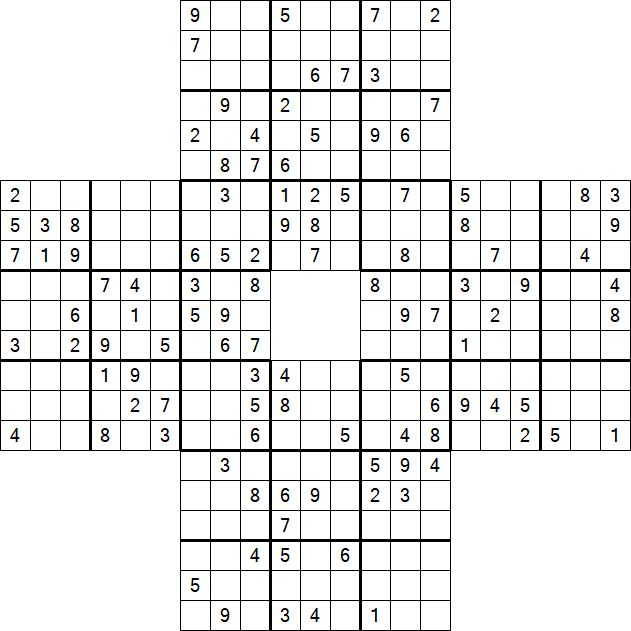
O Sohei Sudoku é uma variante do Sudoku clássico, nomeado em homenagem aos monges guerreiros (Sohei) do Japão medieval. Este quebra-cabeça consiste em quatro grades de Sudoku individuais que são fundidas de forma a compartilhar algumas regiões entre si, criando um quebra-cabeça maior e interconectado. Cada grade tem duas áreas que se sobrepõem com as grades adjacentes, tornando o processo de resolução entrelaçado e dependente das soluções das grades vizinhas.
Regras Básicas
- Estrutura da Grade: O quebra-cabeça consiste em quatro grades 9x9, cada uma com suas próprias linhas, colunas e caixas.
- Números de 1 a 9: Cada linha, coluna e caixa 3x3 dentro de cada grade 9x9 deve conter os números de 1 a 9, sem repetição.
- Áreas de Sobreposição: As grades são conectadas através de áreas de sobreposição que devem obedecer às regras em todas as grades interconectadas.
Regras Adicionais
- Soluções Interconectadas: As áreas de sobreposição significam que resolver uma região particular em uma grade afetará as soluções na grade adjacente. Os números colocados nas áreas de sobreposição devem obedecer às regras do Sudoku para ambas as grades das quais fazem parte.
Dicas Básicas de Resolução
- Comece pelos Números Dados: Comece focando nas grades ou unidades com mais números dados, pois elas fornecerão o ponto de partida mais fácil para determinar onde os outros números podem ir.
- Olhe para as Sobreposições: Dê uma atenção especial às áreas de sobreposição entre as grades, pois elas fornecerão links cruciais entre as soluções de diferentes grades.
- Use Estratégias Clássicas: Empregue estratégias clássicas de Sudoku, como procurar por solteiros, pares apontando e redução de linha de caixa, dentro de cada grade individual.
- Resolução Interconectada: Lembre-se de que resolver uma região em uma grade afetará as soluções possíveis na grade adjacente. Sempre verifique as implicações de colocar um número nas áreas de sobreposição em ambas as grades.
- Mantenha a Consistência: Certifique-se de que as soluções são consistentes em todas as grades interconectadas, especialmente nas áreas de sobreposição.