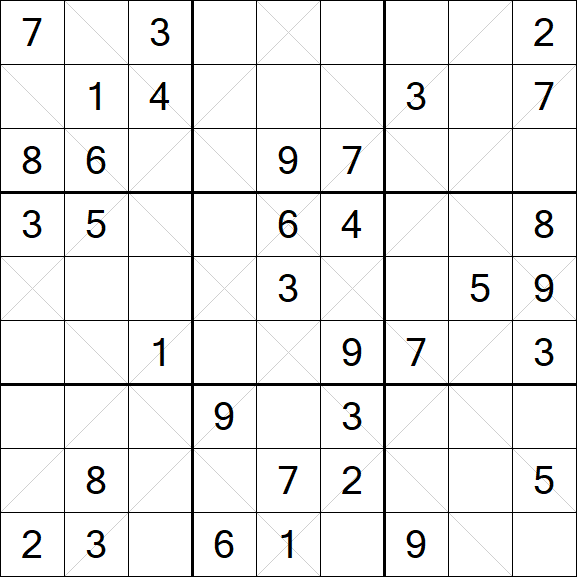
Argyle Sudoku – Medium

To print multiple puzzles at once, click here.

Argyle Sudoku is a variant of the classic Sudoku, a number placement puzzle primarily presented in a 9 x 9 grid, which is further divided into 3 x 3 subgrids, often referred to as "regions". Some cells are pre-filled with numbers, which are referred to as "givens". The main objective is to fill the empty cells in such a way that each column, row, and region contains the numbers 1 through 9, ensuring each number appears exactly once.

Basic Rules

1. Grid Structure: The puzzle consists of a 9 x 9 grid, and this larger grid is subdivided into nine 3 x 3 subgrids or regions.
2. Givens: Some cells are pre-filled with numbers, known as "givens", which are to be used as clues.
3. Number Placement: The solver must fill in the empty cells with numbers 1 through 9.

Additional Rules for Argyle Sudoku

1. Diagonal Lines: In addition to the basic Sudoku rules, Argyle Sudoku introduces marked diagonal lines across the grid.
2. Unique Diagonals: Each digit from 1 to 9 must appear not more than once in these marked diagonal lines.

Basic Solving Tips

1. Single Possibility: If a cell is the only one in its row, column, or region that can contain a particular number, then it must contain that number.
2. Elimination: Exclude numbers that are already present in a row, column, or region from being placed in other cells of that respective row, column, or region.
3. Double Pairs: If two cells in a row, column, or region can only be two numbers (e.g., 3 and 6), then exclude these two numbers from other cells in that respective row, column, or region.
4. Look for Grid Symmetry: Often, the givens and the diagonal lines in Argyle Sudoku have a symmetrical pattern. Utilize this symmetry to anticipate number placements.
5. Utilize the Diagonals: Pay extra attention to the diagonal lines and ensure that you are not repeating any numbers along them.