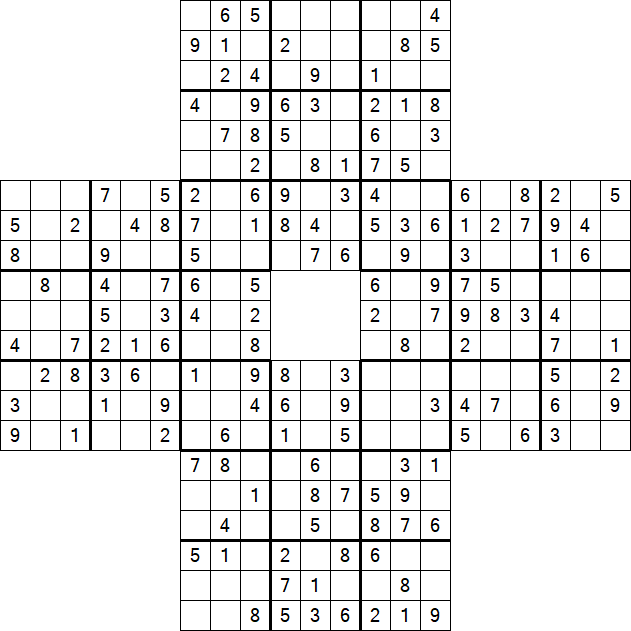
Sohei Sudoku – Medium

To print multiple puzzles at once, click here.

Sohei Sudoku is a variant of the classic Sudoku, named after the warrior monks (Sohei) of medieval Japan. This puzzle consists of four individual Sudoku grids that are merged in a way that they share some regions with each other, creating a larger, interconnected puzzle. Each grid has two overlapping areas with adjacent grids, making the solving process intertwined and dependent on the solutions of the neighboring grids.

Basic Rules

1. Grid Structure: The puzzle consists of four 9x9 grids, each with its own rows, columns, and boxes.
2. Numbers 1-9: Each row, column, and 3x3 box within each 9x9 grid must contain the numbers 1 through 9, without repetition.
3. Overlapping Areas: The grids are connected through overlapping areas which must obey the rules across all interconnected grids.

Additional Rules

• Interconnected Solutions: The overlapping areas mean that solving for a particular region in one grid will affect the solutions in the adjacent grid. The numbers placed in the overlapping areas must obey the Sudoku rules for both grids that they are part of.

Basic Solving Tips

• Start with Given Numbers: Begin by focusing on the grids or units with the most given numbers, as they will provide the easiest starting point for determining where other numbers can go.
• Look for Overlaps: Pay special attention to the overlapping areas between grids, as these will provide crucial links between the solutions of different grids.
• Use Classic Strategies: Employ classic Sudoku strategies, such as looking for singles, pointing pairs, and box-line reduction, within each individual grid.
• Interconnected Solving: Remember that solving a region in one grid will affect the possible solutions in the adjacent grid. Always check the implications of placing a number in the overlapping areas on both grids.
• Keep Consistency: Ensure that the solutions are consistent across all interconnected grids, especially in the overlapping areas.