Windoku – Easy
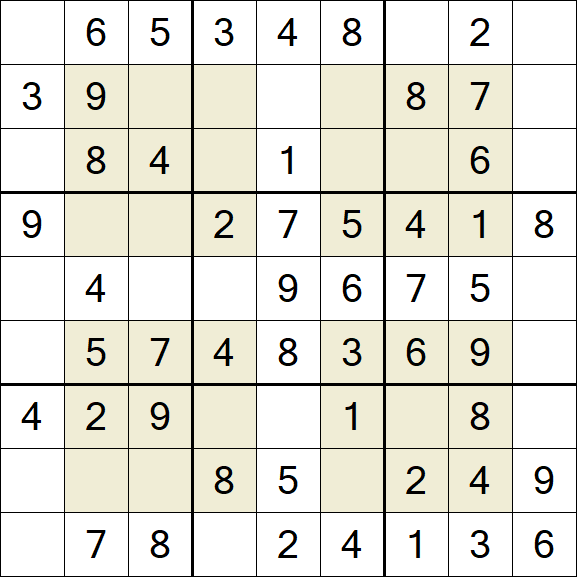
Download puzzle & solution
Share puzzle
Our puzzles are completely free. Please support this website by recommending it to your friends and family. Thank you!
New puzzle
About Windoku
Windoku, also known as "Four-Box Sudoku" or "Hyper Sudoku," is a variant of the classic Sudoku, a number placement puzzle. The standard format involves a 9x9 grid, subdivided into 3x3 subgrids (referred to as "regions"). Some cells are pre-filled with numbers, termed "givens." The objective is to fill the empty cells in such a way that each column, row, and region contains the numbers 1 through 9, with no repetition. The name "Sudoku" implies "single numbers" since each number must appear exactly once in each of the three "directions" (row, column, and region). Windoku introduces an additional layer of complexity with four extra 3x3 areas that also need to contain the numbers 1 to 9 exactly once.
Basic Rules
- Grid Structure: The puzzle consists of a 9x9 grid, divided into 3x3 regions.
- Givens: Some cells contain pre-filled numbers, known as "givens."
- Number Placement: The player must fill in the empty cells with numbers 1 through 9.
- No Repetition: Each number 1-9 must appear exactly once in each row, column, and region.
Additional Rules for Windoku
- Additional Areas: Besides the standard regions, there are four additional 3x3 areas.
- Unique Numbers in Additional Areas: The numbers 1 through 9 must appear exactly once in each of the additional 3x3 areas.
Basic Solving Tips
- Single Possibility: If a cell is the only one in its row, column, or region that can contain a particular number, that number goes in that cell.
- Exclusion: If a number is already present in a row or column, other cells in that row or column in the same region cannot contain that number.
- Double Pairs: If two cells in a row, column, or region can only be two numbers (e.g., 3 and 6), then exclude these two numbers from other cells in that row, column, or region.
- Look for Grid Symmetry: Often, Windoku puzzles exhibit a form of symmetry in the given numbers. Identifying this can help predict the placement of other numbers.
- Utilize the Additional Areas: Remember to consider the additional 3x3 areas when determining possible numbers for a cell.