Girandola Sudoku – Medium
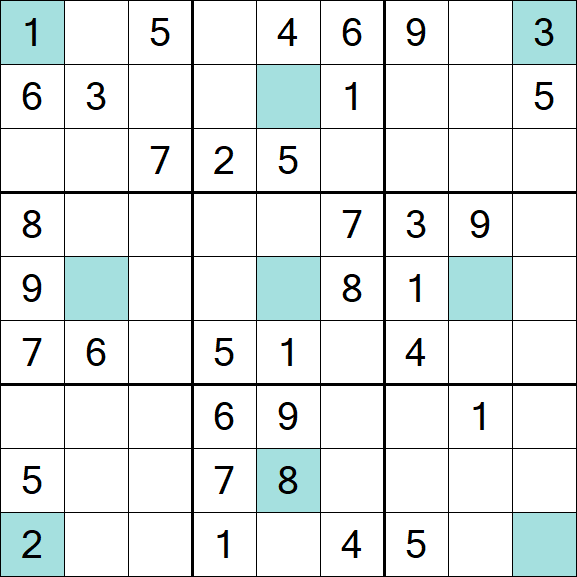
Download puzzle & solution
Share puzzle
Our puzzles are completely free. Please support this website by recommending it to your friends and family. Thank you!
New puzzle
About Girandola Sudoku
Girandola Sudoku is a variant of the classic Sudoku, a number-placement puzzle that is widely recognized and enjoyed by many puzzle enthusiasts. The classic Sudoku is typically a 9x9 grid, divided into 3x3 subgrids, also known as "regions". Some of the cells in the grid are pre-filled with numbers, which are referred to as "givens". The objective is to fill the empty cells in such a way that each row, column, and region contains the numbers 1 through 9, without repetition. Girandola Sudoku introduces an additional twist with an extra group of cells that also need to adhere to the rule of containing digits 1 through 9 without repetition.
Basic Rules
- Grid Structure: The puzzle consists of a 9x9 grid, and this grid is further divided into nine 3x3 subgrids or regions.
- Givens: Some cells are pre-filled with numbers, known as "givens", which provide solvers with starting points.
- Number Placement: The solver must fill in the empty cells with numbers 1 through 9.
Additional Rules for Girandola Sudoku
- Extra Group: In addition to the standard rules, Girandola Sudoku features an extra group of cells, often arranged in a pattern (commonly a circle or a star), which must also contain the digits 1 through 9 without repetition.
Basic Solving Tips
- Single Possibility: If a cell is the only one in its row, column, or region that can contain a particular number, that number goes in the cell.
- Elimination: Exclude numbers from consideration for a particular cell based on the numbers already present in the cell’s row, column, and region.
- Double Pairs: If two cells in a row, column, or region can only be two numbers (a pair), then those two numbers can be excluded from consideration for other cells in that row, column, or region.
- Look for Grid Symmetry: Often, the givens and the extra group in Girandola Sudoku are arranged in a symmetrical pattern, which may help in deducing the logical placement of numbers.